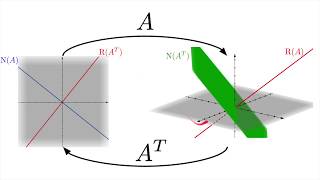
The deeper meaning of matrix transpose
100k Q&A: https://forms.gle/dHnWwszzfHUqFKny7
Transpose isn’t just swapping rows and columns it’s more about changing perspective to get the same measurements. By understanding the general idea of transpose of a linear map, we can use it to visualise transpose much more directly. We will also heavily rely on the concept of covectors, and touch lightly on metric tensors in special/general relativity, and adjoints in quantum mechanics.
As far as I know, this way of visualisation of transpose is original. Most people use SVD (singular value decomposition) for such visualisation, but I think it is much less direct than this one, and also SVD is mostly used for numerical methods, so it feels somewhat unnatural to use a numerical method to explain linear transformations (though, of course, SVD is extremely useful). Please let me know if you know that other people have this specific visualisation.
The concept I am introducing here is usually called a “pullback” (and actually the original linear transformation would be called “pushforward”), but as said in the video, another way of thinking about transpose is the notion of “adjoint”.
Notes:
(1) I am calling covectors a “measuring device”, not only because the level set representation of covectors looks like a ruler when you take a strip of the plane, but also because of its connections with quantum mechanics. A “bra” in quantum mechanics is a covector, and can be thought of as a “measurement”, in the sense of “how likely will you measure that state” (sort of).
(2) I deliberately don’t use row vectors to describe covectors, not only because this only works in finitedimensional spaces, but also because it is awkward for the ordering when we say a transpose matrix acts on the covector. We usually apply transformations on the *left*, but if you treat the covector as a row vector, you have to act the transpose matrix on the *right*.
(3) You can do the sort of “exercise” to verify this visualisation of transpose for all (nonsingular) matrices, but I think the algebra is slightly too tedious. This is the reason why I spent a lot of time talking about the big picture of transpose to make the explanation as natural as possible.
Further reading:
*GENERAL*
(a) Transpose of a linear map (Wikipedia)
https://en.wikipedia.org/wiki/Transpo...
(b) Vector space not isomorphic to its dual (for infinitedimensional vector spaces):
https://math.stackexchange.com/questi...
https://math.stackexchange.com/questi...
*RELATIVITY*
(a) Metric / inverse metric as the vectorcovector correspondence: https://en.wikipedia.org/wiki/Raising...
https://en.wikipedia.org/wiki/Minkows...
*ADJOINT*
(a) Inner product (the prerequisite of even defining adjoints, the analog of dot products in Euclidean space): https://en.wikipedia.org/wiki/Inner_p...
(b) Adjoints (another way of thinking about transposes, but I think this is mostly about the complex analogue of transpose): https://en.wikipedia.org/wiki/Hermiti...
(c) Reisz representation theorem (more relevant to adjoints, but in regards to the statement that “we choose certain covectors to act on”: here, it is the “continuous” dual, very relevant in QM): https://en.wikipedia.org/wiki/Riesz_r...
(d) Selfadjoint operators (Hermitian operators in QM, but also useful in SturmLiouville theory in ODEs):
https://en.wikipedia.org/wiki/Selfad...
Video chapters:
00:00 Introduction
00:56 Chapter 1: The big picture
04:29 Chapter 2: Visualizing covectors
09:32 Chapter 3: Visualizing transpose
16:18 Two other examples of transpose
19:51 Chapter 4: Subtleties (special relativity?)
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:
https://forms.gle/QJ29hocF9uQAyZyH6
If you want to know more interesting Mathematics, stay tuned for the next video!
SUBSCRIBE and see you in the next video!
If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!
Social media:
Facebook: / mathemaniacyt
Instagram: / _mathemaniac_
Twitter: / mathemaniacyt
Patreon: / mathemaniac (support if you want to and can afford to!)
Merch: https://mathemaniac.myspreadshop.co.uk
Kofi: https://kofi.com/mathemaniac [for onetime support]
For my contact email, check my About page on a PC.
See you next time!